3. ЛУННАЯ ГРАВИТАЦИЯ И ЕЕ ВЛИЯНИЕ НА ЗЕМЛЮ

: параметры лунной гравитации : : влияние на тело Земли : : влияние на орбиту Земли : : краткое резюме :

В данной главе мы рассмотрим, как Луна воздействует своим гравитационным полем собственно на саму Землю, т.е. на ее тело и ее движение по орбите. Последствия данного воздействия для различных земных сфер - литосферы, гидросферы, ядра, атмосферы, магнитосферы и др., а также для биосферы будут рассмотрены в следующих главах.

 

ВНИМАНИЕ!
Графики гравитационного взаимодействия Луны и Земли см. с помощью сервиса
ЛУННЫЙ ФАКТОР

 

Расчетные соотношения и константы

Для расчета гравитационного воздействия Луны воспользуемся формулой классической физики, определяющей силу F взаимного притяжения двух тел с массами M1 и M2, центры масс которых находятся друг от друга на расстоянии R:

 

(1) F (н) = (G x M1 x M2) / R²,

 

где G = 6,67384 х 10 ^-11 - гравитационная постоянная.

 

Данная формула дает значение силы притяжения в единицах системы СИ - ньютонах (н). Для целей нашего трактата удобнее и понятнее будет оперировать килограммами силы (кгс), которые получаются делением F на коэффициент 9,81, т.е.:

 

(2) F (кгс) = (G x M1 x M2) / (9,81 х R²)

 

Для дальнейших расчетов нам потребуются следующие константы:

1. масса Луны - 7,35 х 10²² кг;
2. среднее расстояние от Земли до Луны - 384400 км;
3. средний радиус Земли - 6371 км;
4. масса Солнца - 1,99 х 10³⁰ кг;
5. среднее расстояние от Земли до Солнца - 149,6 млн. км;

Сила лунного притяжения на Земле

В соответствии с формулой (2), сила притяжения Луной тела массой 1 кг, находящегося в центре Земли, при расстоянии между Луной и Землей, равном его среднему значению, равна:

 

(3) F = (6,67 х 10 ^-11 х 7,35 х 10²² х 1) / (9,81 х 384400000 ²) = 0, 000003382 кгс

 

т.е. всего 3,382 микрограмма. Для сравнения расчитаем силу притяжения того же тела Солнцем (также для среднего расстояния):

 

(4) F = (6,67 х 10 ^-11 х 1,99 х 10³⁰ х 1) / (9,81 х 149600000000 ²) = 0, 000604570 кгс,

 

т.е. 604,570 микрограмм, что почти в 200 (двести!) раз больше, чем сила притяжения Луной.

Кроме того, вес тела, находящегося на поверхности Земли, изменяется в гораздо более существенных пределах из-за отклонения формы Земли от идеальной, неравномерности рельефа и плотности, а также влияния центробежных сил. Так, например, вес тела массой в 1 кг на полюсах больше веса на экваторе примерно на 5,3 грамма, причем одна треть этой разницы обусловлена сплюснутостью Земли с полюсов, а две трети - центробежной силой на экваторе, направленной против силы тяжести.

 

Как видно, прямое гравитационное воздействие Луны на конкретное тело, находящееся на Земле, является в прямом смысле микроскопическим и при этом существенно уступает гравитационному воздействию Солнца и геофизических аномалий.

 

Градиент силы лунного притяжения

Обратимся к рис.3.1. Для среднего значения расстояния Земля - Луна сила притяжения Луной тела массой 1 кг, расположенного на поверхности Земли в ближайшей к Луне точке составляет 3,495 микрограмм, что на 0,113 микрограмм больше, чем сила притяжения того же тела, но расположенного в центре Земли. Сила же притяжения тела, находящегося на поверхности Земли, Солнцем (также для среднего значения расстояния) составит 604,622 микрограмма, что больше силы притяжения того же тела, но расположенного в центре Земли, на 0,052 микрограмма.

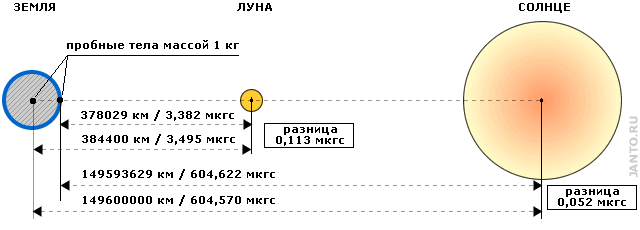
Рис.3.1 Лунная и солнечная гравитация

 

Т.о, несмотря на неизмеримо меньшую массу Луны по сравнению с Солнцем, градиент силы ее тяготения на орбите Земли в среднем в два с лишним раза больше градиента силы тяготения Солнца.

 

Для иллюстрации воздействия гравитационного поля Луны на тело Земли обратимся к рис. 3.2.

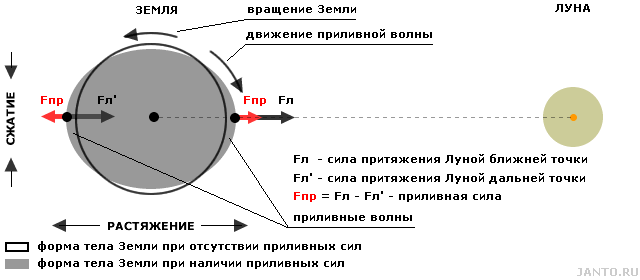
Рис.3.2 Влияние гравитационного поля Луны на тело Земли.

 

Данный рисунок представляет весьма и весьма упрощенную картину реакции тела Земли на воздействие лунной гравитации, но достоверно отражает суть процесса - изменение формы земного шара под воздействием т.н. приливных (или приливообразующих) сил, направленных вдоль оси Земля - Луна, и противодействующих им сил упругости тела Земли. Приливные силы возникают из-за того, что точки Земли, расположенные ближе к Луне, притягиваются к ней сильнее, чем точки, расположенные дальше от нее. Иными словами, деформация тела Земли является следствием градиента силы притяжения Луны и противодействующих ему сил упругости тела Земли. В результате действия этих сил размер Земли увеличивается в направлении действия приливных сил и уменьшается в поперечном направлении, вследствие чего на поверхности образуется волна, именуемая приливной. Эта волна имеет два максимума, находящиеся на оси Земля - Луна и перемещающиеся по поверхности Земли в направлении, противоположном направлению ее вращения. Амплитуда волны зависит от широты местности и текущих параметров орбиты Луны и может достигать нескольких десятков сантиметров. Максимальное значение она будет иметь на экваторе при прохождении Луной ее перигея.

Солнце также вызывает приливную волну в теле Земли, но существенно меньшую из-за меньшего градиента силы его тяготения. Совместное гравитационное воздействие Луны и Солнца на тело Земли зависит от их взаимного расположения. Максимально значение приливных сил и, соответственно, максимальная амплитуда приливной волны достигается при расположении всех трех объектов на одной оси, т.е. в состоянии т.н. сизигии (выравнивания), что имеет место при новолунии (Луна и Солнце в «соединении») или при полнолунии (Луна и Солнце в «оппозиции»). Данные конфигурации иллюстрируются рис. 3.3 и 3.4.

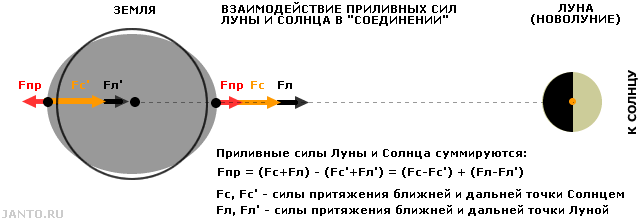
Рис.3.3 Совместное влияние гравитационных полей Луны и Солнца на тело Земли
в «соединении» (в новолуние).

 

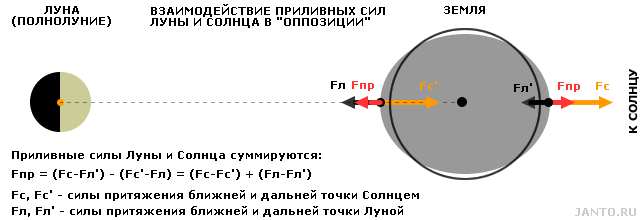
Рис.3.4 Совместное влияние гравитационных полей Луны и Солнца на тело Земли
в «оппозиции» (в полнолуние).

 

По мере отклонения Луны и Солнца от линии сизигии вызываемые ими приливные силы и, соответственно, приливные волны начинают приобретать самостоятельный характер, их сумма уменьшается, а степень их противодействия друг другу растет. Противодействие достигает максимума, когда угол между направлениями на Луну и Солнце из центра Земли равен 90°, т.е. данные тела находятся в «квадрате», а Луна, соответственно, находится в фазе четверти (первой или последней). В этой конфигурации приливные силы Луны и Солнца действуют на форму тела Земли строго противоположно, соответствующие приливные волны на поверхности максимально разнесены, а их амплитуда минимальна, что иллюстрируется рис. 3.5.

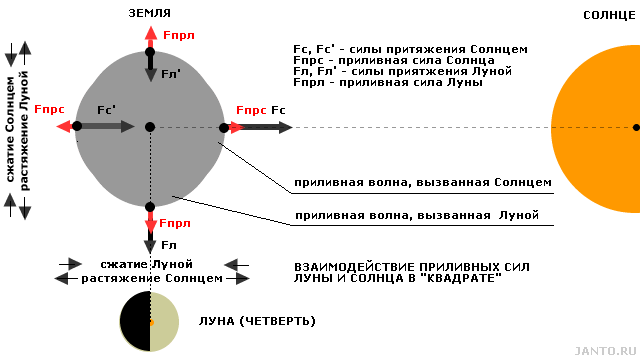
Рис.3.5 Совместное влияние гравитационных полей Луны и Солнца на тело Земли в «квадрате».

 

Примечание. «Соединение», «оппозиция», «квадрат» (или «квадратура») - термины, используемые в астрономии и астрологии для определения геометрии взаимного расположения двух небесных тел или точек относительно Земли. Подробнее см. Лунные аспекты.

 

Физика земных приливных процессов под воздействием гравитационных полей Луны и Солнца весьма сложна и требует учета большого числа параметров. На эту тему было разработано большое число различных теорий, проведено много экспериментальных исследований, написано огромное количество статей, монографий и диссертаций. Даже на сегодняшней день в этой области остается много «белых» пятен, противоречащих друг другу точек зрения и альтернативных подходов. Для желающих углубиться в проблематику земных приливов можно рекомендовать фундаментальное исследование П. Мельхиора «Земные приливы» (пер. с англ., М., «Мир», 1968 г. 483 страницы).

 

 

 

 

Как было отмечено в п.1.1 главы 1, Луна для естественного спутника планеты обладает аномально большой массой, поэтому более корректно считать, что Земля и Луна образуют двойную планетную систему, вращающуюся вокруг общего центра масс, который смещен относительно центра Земли в среднем на 4670 км. Вследствие этого Земля, вращаясь вокруг своей центральной оси, одновременно вращается и вокруг этого центра масс с периодом, равным синодическому лунному месяцу, т.е. 29,530588 солнечных суток. В результате на эллиптическую орбиту Земли накладывается переменнная «модулирующая» составляющая с соответствующей амплитудой и периодом (см. рис.3.6).

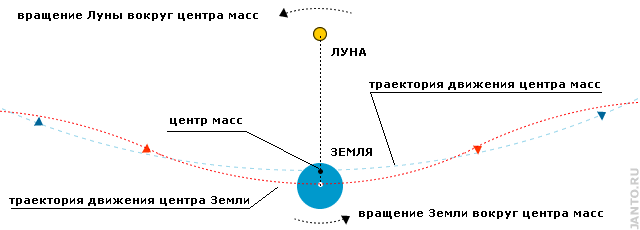
Рис.3.6 Модуляция орбиты Земли лунной гравитацией

 

Эта составляющая изменяет расстояние от Земли до Солнца, что приводит к колебаниям солнечной гравитации примерно на ± 450 мкгс, практически не влияя на ее градиент. Кроме того, она создает определенные силы инерции, внося дополнительный вклад в изменение силы тяжести в зависимости от положения тела на поверхности Земли, а также незначительно влияет на величину достигающей Земли солнечной энергии (см. здесь).

 

Следствием воздействия лунной гравитации на Землю являются два фундаментальных явления:

1. Лунные приливы на поверхности Земли - периодических изменений уровня земной поверхности, синхронизированные с суточным вращением Земли и перемещением Луны по орбите.
2. Наложение на земную орбиту переменной составляющей, синхронизированной с вращением системы Земля - Луна вокруг общего центра масс.

Данные явления являются главными механизмами воздействия Луны на земные сферы - литосферу, гидросферу, земное ядро, атмосферу, магнитосферу и др. Более подробно об этом - в следующей главе.

* * * * *

 

 

Опубликовано 06.08.2015. Последнее изменение - нет.

© Janto 2015 Все права защищены