2. ДВИЖЕНИE ЛУНЫ ПО ОРБИТЕ
Внимание! Базовые сведения о Луне и ее параметрах см. на странице Луна как небесное тело. Лунные фазы, апогеи, перигеи и положение в Зодиаке см. на странице Лунный фактор: данные проекта Лаборатория Геокосмоса.
2.1. ЛУНА И ВТОРОЙ ЗАКОН КЕПЛЕРА
В соответствии со Вторым законом Кеплера каждое небесное тело движется по своей орбите таким образом, что фокальный радиус, соединяющий его с фокусом, являющимся центром вращения, за равные промежутки времени описывает сектора равной площади (см. рис.2.1). В современной интерпретации это следует из закона сохранения момента количества движения J (именуется также моментом импульса, орбитальным моментом или угловым моментом), определяемым, как произведение массы тела m на его скорость v и радиус орбиты r, т.е.
J = m*v*r = const (размерность кгм^2/с).
Отсюда при постоянной массе тела следует:
v*r = const,
т.е. орбитальная скорость тела обратно пропорциональна его удаленности от центра вращения. Поскольку площадь сектора, описываемого за интервал времени Δt фокальным радиусом пропорциональна его длине и длине дуги сектора, а последняя пропорциональна орбитальной скорости тела, т.е. в соответствии с вышеприведенной формулой обратно пропорциональна радиусу сектора, то площадь последнего от данных параметров не зависит и при постоянной массе тела будет постоянна, что и постулирует Второй закон Кеплера.
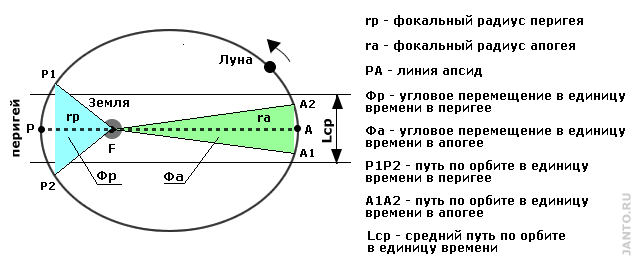
Рис.2.1. Движение Луны по орбите по Второму закону Кеплера
В результате в апогее, где фокальный радиус орбиты максимален, орбитальная и угловая скорости Луны будут минимальны, а в перигее, где фокальный радиус орбиты минимален, максимальны. Соответственно, по мере приближения Луны к перигею ее орбитальная и угловая скорости будут расти, а по мере удаления от перигея - падать.
Это качественная оценка действия Второго закона Кеплера. Его использование для количественной оценки параметров линейной и угловой скоростей движения Луны по орбите сопряжено с необходимостью учитывать, как минимум, влияние таких факторов, как солнечная гравитация и вращение системы Земля-Луна вокруг общего барицентра, т.к. они существенно воздействуют на уазанные параметры, что будет показано ниже.
2.2. ДИНАМИКА ДВИЖЕНИЯ ЛУНЫ ПО ОРБИТЕ
Средняя орбитальная скорость Луны обычно принимается равной 1.02 км/с. Однако она нас практически не интересует, т.к. главной задачей настоящей работы является описание особенностей видимого движения Луны по небесной сфере, а оно определяется угловым перемещением Луны по орбите, ее траекторией и их долговременными вариациями под воздействием прецессий лунной орбиты.
Средняя угловая скорость движения Луны по орбите может быть определена делением угла полного оборота (360 °) на сидерический период, выраженный в сутках, часах или минутах. Соответственно получаем среднее угловое перемещение Луны:
- за сутки - 13,1763 °(13 °10'31");
- за час - 0,549 ° (32'56");
- за минуту - 0,0092 ° (33").
Для нас наибольший интерес представляет суточное угловое перемещение Луны, в т.ч. его вариации в апогеях и перигеях и при перемещении между ними.
Суточное угловое перемещение Луны для каждого значения радиусов апогея и перигея можно было бы вычислять по закону Кеплера, опираясь на величину углового перемещения для какого-нибудь базового фокального радиуса, если бы не влияние упомянутых выше возмущающих факторов Солнца и Земли. Как будет показано ниже, неучет этих факторов дает достаточно большую погрешность. Поэтому наиболее приемлемо принять за угловое перемещение Луны по орбите ее угловое перемещение вдоль эклиптики в эклиптической системе координат. В силу незначительного наклона плоскости орбиты Луны к плоскости эклиптики (4.983 - 5.317°) погрешность при этом составит не более нескольких долей процента, что для наших задач более, чем достаточно.
Для оценки динамики движения Луны по орбите на основе указанного допущения был произведен расчет суточного углового перемещения Луны в апогеях и перигеях за период 2016 - 2022 г.г. Для расчета использовались таблицы тропических эфемерид Asrodients (см. раздел Астрофактор проекта Лаборатория Геокосмоса). Результаты данного расчета приведены в таблице 2.1.
Таблица 2.1
NR |
ДАТА |
AP |
ra км |
rp км |
по Кеплеру |
по эфемеридам |
wa° |
wp° |
Δ° |
wa° |
wp° |
Δ° |
| | | | | | | | | | |
| 1 | 2016-01-16 | P | 0 | 369618 | 0 | 14.60 | - | 0 | 14.13 | - |
| 2 | 2016-01-31 | A | 404552 | 0 | 11.84 | 0 | -2.76 | 11.82 | 0 | -2.31 |
| 3 | 2016-02-12 | P | 0 | 364357 | 0 | 14.81 | +2.97 | 0 | 14.60 | +2.78 |
| 4 | 2016-02-28 | A | 405382 | 0 | 11.82 | 0 | -2.99 | 11.82 | 0 | -2.78 |
| 5 | 2016-03-11 | P | 0 | 359508 | 0 | 15.01 | +3.19 | 0 | 15.00 | +3.18 |
| 6 | 2016-03-26 | A | 406123 | 0 | 11.80 | 0 | -3.21 | 11.82 | 0 | -3.18 |
| 7 | 2016-04-08 | P | 0 | 357163 | 0 | 15.11 | +3.31 | 0 | 15.23 | +3.41 |
| 8 | 2016-04-22 | A | 406350 | 0 | 11.79 | 0 | -3.32 | 11.82 | 0 | -3.41 |
| 9 | 2016-05-07 | P | 0 | 357827 | 0 | 15.08 | +3.29 | 0 | 15.22 | +3.40 |
| 10 | 2016-05-19 | A | 405933 | 0 | 11.80 | 0 | -3.28 | 11.80 | 0 | -3.42 |
| 11 | 2016-06-04 | P | 0 | 361141 | 0 | 14.94 | +3.14 | 0 | 14.97 | +3.17 |
| 12 | 2016-06-16 | A | 405021 | 0 | 11.83 | 0 | -3.11 | 11.83 | 0 | -3.14 |
| 13 | 2016-07-02 | P | 0 | 365982 | 0 | 14.74 | +2.91 | 0 | 14.58 | +2.75 |
| 14 | 2016-07-14 | A | 404271 | 0 | 11.85 | 0 | -2.89 | 11.87 | 0 | -2.71 |
| 15 | 2016-07-28 | P | 0 | 369658 | 0 | 14.60 | +2.75 | 0 | 14.22 | +2.35 |
| 16 | 2016-08-11 | A | 404265 | 0 | 11.85 | 0 | -2.75 | 11.87 | 0 | -2.35 |
| 17 | 2016-08-23 | P | 0 | 367046 | 0 | 14.70 | +2.85 | 0 | 14.40 | +2.53 |
| 18 | 2016-09-07 | A | 405057 | 0 | 11.83 | 0 | -2.87 | 11.85 | 0 | -2.55 |
| 19 | 2016-09-19 | P | 0 | 361893 | 0 | 14.91 | +3.08 | 0 | 14.87 | +3.02 |
| 20 | 2016-10-05 | A | 406099 | 0 | 11.80 | 0 | -3.11 | 11.83 | 0 | -3.04 |
| 21 | 2016-10-17 | P | 0 | 357859 | 0 | 15.08 | +3.28 | 0 | 15.20 | +3.37 |
| 22 | 2016-11-01 | A | 406659 | 0 | 11.78 | 0 | -3.30 | 11.87 | 0 | -3.33 |
| 23 | 2016-11-15 | P | 0 | 356511 | 0 | 15.13 | +3.35 | 0 | 15.37 | +3.50 |
| 24 | 2016-11-28 | A | 406555 | 0 | 11.79 | 0 | -3.34 | 11.85 | 0 | -3.52 |
| 25 | 2016-12-13 | P | 0 | 358462 | 0 | 15.05 | +3.26 | 0 | 15.18 | +3.33 |
| 26 | 2016-12-26 | A | 405869 | 0 | 11.81 | 0 | -3.24 | 11.87 | 0 | -3.31 |
| 27 | 2017-01-11 | P | 0 | 363241 | 0 | 14.85 | +3.04 | 0 | 14.80 | +2.93 |
| 28 | 2017-01-23 | A | 404911 | 0 | 11.83 | 0 | -3.02 | 11.88 | 0 | -2.92 |
| 29 | 2017-02-07 | P | 0 | 368816 | 0 | 14.63 | +2.80 | 0 | 14.33 | +2.45 |
| 30 | 2017-02-19 | A | 404375 | 0 | 11.85 | 0 | -2.78 | 11.88 | 0 | -2.45 |
| 31 | 2017-03-04 | P | 0 | 369063 | 0 | 14.62 | +2.77 | 0 | 14.30 | +2.42 |
| 32 | 2017-03-19 | A | 404650 | 0 | 11.84 | 0 | -2.78 | 11.88 | 0 | -2.42 |
| 33 | 2017-03-31 | P | 0 | 363854 | 0 | 14.83 | +2.99 | 0 | 14.75 | +2.87 |
| 34 | 2017-04-16 | A | 405477 | 0 | 11.82 | 0 | -3.01 | 11.87 | 0 | -2.88 |
| 35 | 2017-04-28 | P | 0 | 359323 | 0 | 15.01 | +3.19 | 0 | 15.15 | +3.28 |
| 36 | 2017-05-13 | A | 406210 | 0 | 11.80 | 0 | -3.21 | 11.87 | 0 | -3.28 |
| 37 | 2017-05-27 | P | 0 | 357209 | 0 | 15.10 | +3.30 | 0 | 15.28 | +3.41 |
| 38 | 2017-06-09 | A | 406401 | 0 | 11.79 | 0 | -3.31 | 11.88 | 0 | -3.40 |
| 39 | 2017-06-24 | P | 0 | 357937 | 0 | 15.07 | +3.28 | 0 | 15.23 | +3.35 |
| 40 | 2017-07-07 | A | 405932 | 0 | 11.80 | 0 | -3.27 | 11.87 | 0 | -3.36 |
| 41 | 2017-07-22 | P | 0 | 361236 | 0 | 14.94 | +3.14 | 0 | 14.93 | +3.06 |
| 42 | 2017-08-03 | A | 405024 | 0 | 11.83 | 0 | -3.11 | 11.87 | 0 | -3.06 |
| 43 | 2017-08-19 | P | 0 | 366127 | 0 | 14.74 | +2.91 | 0 | 14.50 | +2.63 |
| 44 | 2017-08-31 | A | 404305 | 0 | 11.85 | 0 | -2.89 | 11.87 | 0 | -2.63 |
| 45 | 2017-09-14 | P | 0 | 369855 | 0 | 14.59 | +2.74 | 0 | 14.20 | +2.33 |
| 46 | 2017-09-28 | A | 404341 | 0 | 11.85 | 0 | -2.74 | 11.85 | 0 | -2.35 |
| 47 | 2017-10-10 | P | 0 | 366857 | 0 | 14.71 | +2.86 | 0 | 14.48 | +2.63 |
| 48 | 2017-10-26 | A | 405150 | 0 | 11.83 | 0 | -2.88 | 11.82 | 0 | -2.66 |
| 49 | 2017-11-07 | P | 0 | 361437 | 0 | 14.93 | +3.10 | 0 | 14.92 | +3.10 |
| 50 | 2017-11-22 | A | 406131 | 0 | 11.80 | 0 | -3.13 | 11.82 | 0 | -3.10 |
| 51 | 2017-12-05 | P | 0 | 357495 | 0 | 15.09 | +3.29 | 0 | 15.25 | +3.43 |
| 52 | 2017-12-20 | A | 406604 | 0 | 11.78 | 0 | -3.31 | 11.80 | 0 | -3.45 |
| 53 | 2018-01-02 | P | 0 | 356565 | 0 | 15.13 | +3.35 | 0 | 15.30 | +3.50 |
| 54 | 2018-01-16 | A | 406459 | 0 | 11.79 | 0 | -3.34 | 11.82 | 0 | -3.48 |
| 55 | 2018-01-31 | P | 0 | 358994 | 0 | 15.03 | +3.24 | 0 | 15.07 | +3.25 |
| 56 | 2018-02-12 | A | 405700 | 0 | 11.81 | 0 | -3.22 | 11.80 | 0 | -3.27 |
| 57 | 2018-02-28 | P | 0 | 363936 | 0 | 14.82 | +3.01 | 0 | 14.65 | +2.85 |
| 58 | 2018-03-12 | A | 404681 | 0 | 11.84 | 0 | -2.98 | 11.80 | 0 | -2.85 |
| 59 | 2018-03-27 | P | 0 | 369103 | 0 | 14.62 | +2.78 | 0 | 14.20 | +2.40 |
| 60 | 2018-04-09 | A | 404144 | 0 | 11.86 | 0 | -2.76 | 11.82 | 0 | -2.38 |
| 61 | 2018-04-21 | P | 0 | 368712 | 0 | 14.63 | +2.77 | 0 | 14.28 | +2.46 |
| 62 | 2018-05-07 | A | 404457 | 0 | 11.85 | 0 | -2.78 | 11.80 | 0 | -2.48 |
| 63 | 2018-05-18 | P | 0 | 363776 | 0 | 14.83 | +2.98 | 0 | 14.70 | +2.90 |
| 64 | 2018-06-03 | A | 405314 | 0 | 11.82 | 0 | -3.01 | 11.80 | 0 | -2.90 |
| 65 | 2018-06-15 | P | 0 | 359506 | 0 | 15.01 | +3.19 | 0 | 15.03 | +3.23 |
| 66 | 2018-07-01 | A | 406059 | 0 | 11.80 | 0 | -3.21 | 11.78 | 0 | -3.25 |
| 67 | 2018-07-14 | P | 0 | 357431 | 0 | 15.09 | +3.29 | 0 | 15.18 | +3.40 |
| 68 | 2018-07-28 | A | 406222 | 0 | 11.80 | 0 | -3.29 | 11.80 | 0 | -3.38 |
| 69 | 2018-08-11 | P | 0 | 358082 | 0 | 15.07 | +3.27 | 0 | 15.12 | +3.32 |
| 70 | 2018-08-24 | A | 405743 | 0 | 11.81 | 0 | -3.26 | 11.80 | 0 | -3.32 |
| 71 | 2018-09-09 | P | 0 | 361354 | 0 | 14.93 | +3.12 | 0 | 14.87 | +3.07 |
| 72 | 2018-09-21 | A | 404874 | 0 | 11.83 | 0 | -3.10 | 11.82 | 0 | -3.05 |
| 73 | 2018-10-06 | P | 0 | 366395 | 0 | 14.73 | +2.90 | 0 | 14.43 | +2.61 |
| 74 | 2018-10-18 | A | 404225 | 0 | 11.85 | 0 | -2.88 | 11.80 | 0 | -2.63 |
| 75 | 2018-11-01 | P | 0 | 370200 | 0 | 14.57 | +2.72 | 0 | 14.08 | +2.28 |
| 76 | 2018-11-15 | A | 404340 | 0 | 11.85 | 0 | -2.72 | 11.78 | 0 | -2.30 |
| 77 | 2018-11-27 | P | 0 | 366622 | 0 | 14.72 | +2.87 | 0 | 14.42 | +2.64 |
| 78 | 2018-12-13 | A | 405176 | 0 | 11.83 | 0 | -2.89 | 11.78 | 0 | -2.64 |
| 79 | 2018-12-25 | P | 0 | 361059 | 0 | 14.94 | +3.11 | 0 | 14.88 | +3.10 |
| 80 | 2019-01-10 | A | 406114 | 0 | 11.80 | 0 | -3.14 | 11.78 | 0 | -3.10 |
| 81 | 2019-01-22 | P | 0 | 357344 | 0 | 15.10 | +3.30 | 0 | 15.18 | +3.40 |
| 82 | 2019-02-06 | A | 406555 | 0 | 11.79 | 0 | -3.31 | 11.80 | 0 | -3.38 |
| 83 | 2019-02-20 | P | 0 | 356761 | 0 | 15.12 | +3.33 | 0 | 15.27 | +3.47 |
| 84 | 2019-03-05 | A | 406390 | 0 | 11.79 | 0 | -3.33 | 11.78 | 0 | -3.49 |
| 85 | 2019-03-20 | P | 0 | 359380 | 0 | 15.01 | +3.22 | 0 | 15.05 | +3.27 |
| 86 | 2019-04-02 | A | 405576 | 0 | 11.81 | 0 | -3.20 | 11.82 | 0 | -3.23 |
| 87 | 2019-04-17 | P | 0 | 364208 | 0 | 14.81 | +3.00 | 0 | 14.67 | +2.85 |
| 88 | 2019-04-29 | A | 404576 | 0 | 11.84 | 0 | -2.97 | 11.82 | 0 | -2.85 |
| 89 | 2019-05-14 | P | 0 | 369015 | 0 | 14.62 | +2.78 | 0 | 14.27 | +2.45 |
| 90 | 2019-05-27 | A | 404133 | 0 | 11.86 | 0 | -2.76 | 11.83 | 0 | -2.44 |
| 91 | 2019-06-08 | P | 0 | 368506 | 0 | 14.64 | +2.78 | 0 | 14.25 | +2.42 |
| 92 | 2019-06-24 | A | 404548 | 0 | 11.84 | 0 | -2.80 | 11.85 | 0 | -2.40 |
| 93 | 2019-07-06 | P | 0 | 363727 | 0 | 14.83 | +2.99 | 0 | 14.67 | +2.82 |
| 94 | 2019-07-22 | A | 405478 | 0 | 11.82 | 0 | -3.01 | 11.85 | 0 | -2.82 |
| 95 | 2019-08-03 | P | 0 | 359397 | 0 | 15.01 | +3.19 | 0 | 15.05 | +3.20 |
| 96 | 2019-08-18 | A | 406243 | 0 | 11.79 | 0 | -3.22 | 11.85 | 0 | -3.20 |
| 97 | 2019-08-31 | P | 0 | 357175 | 0 | 15.11 | +3.32 | 0 | 15.27 | +3.42 |
| 98 | 2019-09-14 | A | 406377 | 0 | 11.79 | 0 | -3.32 | 11.85 | 0 | -3.42 |
| 99 | 2019-09-29 | P | 0 | 357802 | 0 | 15.08 | +3.29 | 0 | 15.25 | +3.40 |
| 100 | 2019-10-11 | A | 405901 | 0 | 11.80 | 0 | -3.28 | 11.85 | 0 | -3.40 |
| 101 | 2019-10-27 | P | 0 | 361314 | 0 | 14.93 | +3.13 | 0 | 14.98 | +3.13 |
| 102 | 2019-11-08 | A | 405059 | 0 | 11.83 | 0 | -3.10 | 11.85 | 0 | -3.13 |
| 103 | 2019-11-24 | P | 0 | 366720 | 0 | 14.71 | +2.88 | 0 | 14.53 | +2.68 |
| 104 | 2019-12-06 | A | 404445 | 0 | 11.85 | 0 | -2.86 | 11.88 | 0 | -2.65 |
| 105 | 2019-12-19 | P | 0 | 370258 | 0 | 14.57 | +2.72 | 0 | 14.18 | +2.30 |
| 106 | 2020-01-03 | A | 404578 | 0 | 11.84 | 0 | -2.73 | 11.87 | 0 | -2.31 |
| 107 | 2020-01-14 | P | 0 | 365963 | 0 | 14.74 | +2.90 | 0 | 14.55 | +2.68 |
| 108 | 2020-01-30 | A | 405389 | 0 | 11.82 | 0 | -2.92 | 11.87 | 0 | -2.68 |
| 109 | 2020-02-11 | P | 0 | 360463 | 0 | 14.97 | +3.15 | 0 | 15.02 | +3.15 |
| 110 | 2020-02-27 | A | 406276 | 0 | 11.79 | 0 | -3.18 | 11.85 | 0 | -3.17 |
| 111 | 2020-03-11 | P | 0 | 357122 | 0 | 15.11 | +3.32 | 0 | 15.32 | +3.47 |
| 112 | 2020-03-25 | A | 406688 | 0 | 11.78 | 0 | -3.33 | 11.87 | 0 | -3.45 |
| 113 | 2020-04-08 | P | 0 | 356908 | 0 | 15.12 | +3.34 | 0 | 15.35 | +3.48 |
| 114 | 2020-04-21 | A | 406461 | 0 | 11.79 | 0 | -3.33 | 11.87 | 0 | -3.48 |
| 115 | 2020-05-07 | P | 0 | 359655 | 0 | 15.00 | +3.21 | 0 | 15.07 | +3.20 |
| 116 | 2020-05-19 | A | 405583 | 0 | 11.81 | 0 | -3.19 | 11.87 | 0 | -3.20 |
| 117 | 2020-06-04 | P | 0 | 364365 | 0 | 14.81 | +3.00 | 0 | 14.67 | +2.80 |
| 118 | 2020-06-16 | A | 404596 | 0 | 11.84 | 0 | -2.97 | 11.88 | 0 | -2.79 |
| 119 | 2020-07-01 | P | 0 | 368957 | 0 | 14.62 | +2.78 | 0 | 14.27 | +2.39 |
| 120 | 2020-07-13 | A | 404200 | 0 | 11.85 | 0 | -2.77 | 11.88 | 0 | -2.39 |
| 121 | 2020-07-26 | P | 0 | 368366 | 0 | 14.65 | +2.80 | 0 | 14.35 | +2.47 |
| 122 | 2020-08-10 | A | 404657 | 0 | 11.84 | 0 | -2.81 | 11.87 | 0 | -2.48 |
| 123 | 2020-08-22 | P | 0 | 363512 | 0 | 14.84 | +3.00 | 0 | 14.80 | +2.93 |
| 124 | 2020-09-07 | A | 405605 | 0 | 11.81 | 0 | -3.03 | 11.83 | 0 | -2.97 |
| 125 | 2020-09-19 | P | 0 | 359080 | 0 | 15.03 | +3.22 | 0 | 15.15 | +3.32 |
| 126 | 2020-10-04 | A | 406319 | 0 | 11.79 | 0 | -3.24 | 11.85 | 0 | -3.30 |
| 127 | 2020-10-17 | P | 0 | 356912 | 0 | 15.12 | +3.33 | 0 | 15.30 | +3.45 |
| 128 | 2020-10-31 | A | 406392 | 0 | 11.79 | 0 | -3.33 | 11.87 | 0 | -3.43 |
| 129 | 2020-11-15 | P | 0 | 357838 | 0 | 15.08 | +3.29 | 0 | 15.20 | +3.33 |
| 130 | 2020-11-28 | A | 405890 | 0 | 11.81 | 0 | -3.27 | 11.83 | 0 | -3.37 |
| 131 | 2020-12-13 | P | 0 | 361776 | 0 | 14.91 | +3.10 | 0 | 14.83 | +3.00 |
| 132 | 2020-12-25 | A | 405009 | 0 | 11.83 | 0 | -3.08 | 11.82 | 0 | -3.01 |
| 133 | 2021-01-10 | P | 0 | 367389 | 0 | 14.69 | +2.86 | 0 | 14.37 | +2.55 |
| 134 | 2021-01-22 | A | 404360 | 0 | 11.85 | 0 | -2.84 | 11.82 | 0 | -2.55 |
| 135 | 2021-02-04 | P | 0 | 370126 | 0 | 14.58 | +2.73 | 0 | 14.15 | +2.33 |
| 136 | 2021-02-19 | A | 404465 | 0 | 11.85 | 0 | -2.73 | 11.82 | 0 | -2.33 |
| 137 | 2021-03-03 | P | 0 | 365421 | 0 | 14.76 | +2.91 | 0 | 14.57 | +2.75 |
| 138 | 2021-03-19 | A | 405252 | 0 | 11.82 | 0 | -2.94 | 11.78 | 0 | -2.79 |
| 139 | 2021-03-31 | P | 0 | 360310 | 0 | 14.97 | +3.15 | 0 | 14.97 | +3.19 |
| 140 | 2021-04-15 | A | 406119 | 0 | 11.80 | 0 | -3.17 | 11.80 | 0 | -3.17 |
| 141 | 2021-04-28 | P | 0 | 357378 | 0 | 15.10 | +3.30 | 0 | 15.22 | +3.42 |
| 142 | 2021-05-12 | A | 406511 | 0 | 11.79 | 0 | -3.31 | 11.80 | 0 | -3.42 |
| 143 | 2021-05-27 | P | 0 | 357309 | 0 | 15.10 | +3.31 | 0 | 15.18 | +3.38 |
| 144 | 2021-06-09 | A | 406228 | 0 | 11.80 | 0 | -3.30 | 11.80 | 0 | -3.38 |
| 145 | 2021-06-24 | P | 0 | 359959 | 0 | 14.99 | +3.19 | 0 | 14.98 | +3.18 |
| 146 | 2021-07-06 | A | 405341 | 0 | 11.82 | 0 | -3.17 | 11.78 | 0 | -3.20 |
| 147 | 2021-07-22 | P | 0 | 364519 | 0 | 14.80 | +2.98 | 0 | 14.60 | +2.82 |
| 148 | 2021-08-03 | A | 404410 | 0 | 11.85 | 0 | -2.95 | 11.80 | 0 | -2.80 |
| 149 | 2021-08-18 | P | 0 | 369126 | 0 | 14.62 | +2.77 | 0 | 14.18 | +2.38 |
| 150 | 2021-08-31 | A | 404098 | 0 | 11.86 | 0 | -2.76 | 11.80 | 0 | -2.38 |
| 151 | 2021-09-12 | P | 0 | 368463 | 0 | 14.64 | +2.78 | 0 | 14.25 | +2.45 |
| 152 | 2021-09-27 | A | 404639 | 0 | 11.84 | 0 | -2.80 | 11.80 | 0 | -2.45 |
| 153 | 2021-10-09 | P | 0 | 363387 | 0 | 14.85 | +3.01 | 0 | 14.70 | +2.90 |
| 154 | 2021-10-25 | A | 405614 | 0 | 11.81 | 0 | -3.04 | 11.78 | 0 | -2.92 |
| 155 | 2021-11-06 | P | 0 | 358844 | 0 | 15.03 | +3.22 | 0 | 15.05 | +3.27 |
| 156 | 2021-11-22 | A | 406275 | 0 | 11.79 | 0 | -3.24 | 11.78 | 0 | -3.27 |
| 157 | 2021-12-05 | P | 0 | 356793 | 0 | 15.12 | +3.33 | 0 | 15.25 | +3.47 |
| 158 | 2021-12-19 | A | 406321 | 0 | 11.79 | 0 | -3.33 | 11.80 | 0 | -3.45 |
| 159 | 2022-01-02 | P | 0 | 358036 | 0 | 15.07 | +3.28 | 0 | 15.13 | +3.33 |
| 160 | 2022-01-15 | A | 405804 | 0 | 11.81 | 0 | -3.26 | 11.78 | 0 | -3.35 |
| 161 | 2022-01-31 | P | 0 | 362249 | 0 | 14.89 | +3.08 | 0 | 14.85 | +3.07 |
| 162 | 2022-02-12 | A | 404896 | 0 | 11.83 | 0 | -3.06 | 11.80 | 0 | -3.05 |
| 163 | 2022-02-27 | P | 0 | 367785 | 0 | 14.67 | +2.84 | 0 | 14.35 | +2.55 |
| 164 | 2022-03-11 | A | 404267 | 0 | 11.85 | 0 | -2.82 | 11.82 | 0 | -2.53 |
| 165 | 2022-03-24 | P | 0 | 369762 | 0 | 14.59 | +2.74 | 0 | 14.15 | +2.33 |
| 166 | 2022-04-08 | A | 404437 | 0 | 11.85 | 0 | -2.74 | 11.82 | 0 | -2.33 |
| 167 | 2022-04-20 | P | 0 | 365142 | 0 | 14.78 | +2.93 | 0 | 14.55 | +2.73 |
| 168 | 2022-05-06 | A | 405286 | 0 | 11.82 | 0 | -2.96 | 11.82 | 0 | -2.73 |
| 169 | 2022-05-18 | P | 0 | 360297 | 0 | 14.97 | +3.15 | 0 | 14.95 | +3.13 |
| 170 | 2022-06-03 | A | 406190 | 0 | 11.80 | 0 | -3.17 | 11.82 | 0 | -3.13 |
| 171 | 2022-06-15 | P | 0 | 357433 | 0 | 15.09 | +3.29 | 0 | 15.18 | +3.36 |
| 172 | 2022-06-30 | A | 406580 | 0 | 11.79 | 0 | -3.30 | 11.83 | 0 | -3.35 |
| 173 | 2022-07-14 | P | 0 | 357263 | 0 | 15.10 | +3.31 | 0 | 15.28 | +3.45 |
| 174 | 2022-07-27 | A | 406274 | 0 | 11.79 | 0 | -3.31 | 11.83 | 0 | -3.45 |
| 175 | 2022-08-11 | P | 0 | 359829 | 0 | 14.99 | +3.20 | 0 | 15.07 | +3.24 |
| 176 | 2022-08-23 | A | 405418 | 0 | 11.82 | 0 | -3.17 | 11.82 | 0 | -3.25 |
| 177 | 2022-09-08 | P | 0 | 364490 | 0 | 14.80 | +2.98 | 0 | 14.68 | +2.86 |
| 178 | 2022-09-20 | A | 404555 | 0 | 11.84 | 0 | -2.96 | 11.85 | 0 | -2.83 |
| 179 | 2022-10-05 | P | 0 | 369334 | 0 | 14.61 | +2.77 | 0 | 14.28 | +2.43 |
| 180 | 2022-10-18 | A | 404329 | 0 | 11.85 | 0 | -2.76 | 11.87 | 0 | -2.41 |
| 181 | 2022-10-30 | P | 0 | 368287 | 0 | 14.65 | +2.80 | 0 | 14.32 | +2.45 |
| 182 | 2022-11-15 | A | 404923 | 0 | 11.83 | 0 | -2.82 | 11.85 | 0 | -2.47 |
| 183 | 2022-11-27 | P | 0 | 362825 | 0 | 14.87 | +3.04 | 0 | 14.78 | +2.93 |
| 184 | 2022-12-13 | A | 405868 | 0 | 11.81 | 0 | -3.06 | 11.85 | 0 | -2.93 |
| 185 | 2022-12-25 | P | 0 | 358269 | 0 | 15.06 | +3.25 | 0 | 15.22 | +3.37 |
ra и rp - радиусы апогея и перигея, wa и wp - суточное угловое перемещение в апогее и перигее, Δ - разница суточных угловых перемещений между последовательными апогеями и перигеями.
Как видно, угловое суточное перемещение Луны в апогее изменяется незначительно - не более, чем на несколько сотых долей градуса. В то же время вариации суточного углового перемещения в перигее достаточно велики и могут достигать более 1 градуса. Наиболее значимые для динамики движения Луны по небесной сфере вариации - при перемещении Луны между апогеями и перигеями. Они могут доходить до 3.5 градусов, т.е. более ± 10 процентов от среднего значения суточного углового перемещения. Для наглядности диаграмма всех указанных вариаций изображена на рис.2.2.
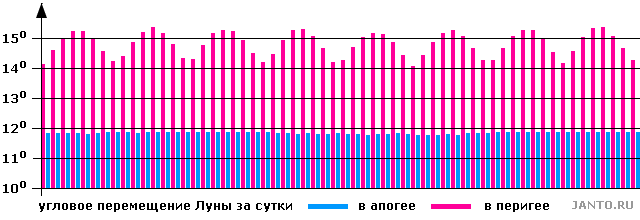
Рис.2.2. Суточное угловое перемещение Луны в апогеях и перигеях
2.3. ОТКЛОНЕНИЕ ОТ ЗАКОНА КЕПЛЕРА
Для оценки степени применимости Второго закона Кеплера для количественного расчета динамики движения Луны в условиях воздействия возмущений Солнца и Земли был произведен расчет ее углового суточного перемещения в двух вариантах.
Вариант 1. За базу принималось произведение произвольно выбранного радиуса апогея или перигея на соответствующее ему суточное угловое перемещение, вычисленное по эклиптическим эфемеридам. Значение суточного углового перемещения для каждого фокального радиуса вычислялось делением базы на величину этого фокального радиуса. Расчет дал приемлемую погрешность для однотипных фокальных радиусов (апогея или перигея), если радиус базы был взят того же типа, и погрешность на уровне 1 - 1,5 для фокальных радиусов противоположного типа.
Вариант 2. Для расчета угловых перемещений в апогее и перигее принимались две базы, в т.ч. для апогея - радиус апогея, близкий к его среднему значению, а для перигея - радиус перигея, близкий к его среднему значени. Результаты расчета по данному варианту приведены в таблице 2.1 (столбцы группы «по Кеплеру»). Как видно, погрешность расчета в данном варианте оказалась на уровне нескольких десятых долей градуса, что в контексте задач настоящей работы можно было бы считать приемлемым результатом, но уступающим по точности расчету с использованием эклиптических эфемерид. Поэтому для дальнейшего анализа будет использован последний.
* * * * *
Опубликовано 09.06.2022. Последнее изменение 09.06.2022.
© Janto 2022 Все права защищены

