1. РЕЗОНАНС ШУМАНА: ПРИНЦИП И ПАРАМЕТРЫ

: вводные замечания : : физический принцип : : трехмерное представление : : частоты резонанса : : спектр и уровни сигналов :

 

Резонансом Шумана называется явление резонанса природных электромагнитных волн в замкнутом волноводе, образованном земной поверхностью и нижними слоями ионосферы. Его существование было теоретически предсказано немецким физиком Вильфридом Отто Шуманом в 1952 году и потом экспериментально обнаружено им же и его сподвижниками. Для правильного настроя на понимание принципа данного явления необходимо сразу же сделать акцент на том, что сигналы резонанса Шумана - это не какие-то самостоятельные сигналы особой природы, генерируемые неким особым источником, а всего лишь сигналы, выделяемые резонансными свойствами волновода Земля-ионосфера из общего природного сверхнизкочастотного электромагнитного шума, создаваемого преимущественно (но не единственно) атмосферными электрическими разрядами.

 

Резонанс Шумана возникает вследствие того, что электромагнитные волны, излучаемые источником, находящимся в волноводе Земля - ионосфера, многократно проходят по нему, огибая земной шар, и при этом накладываются друг на друга, что при встречном движении приводит на определенных частотах к образованию стоячих волн. В большинстве научно-популярных источников этот процесс иллюстрируется простейшей статической двумерной схемой, что является чрезмерным упрощением. Поэтому для более полного и корректного представления о данном резонансе и понимания некоторых важных деталей обратимся к трехмерным моделям, в т.ч. к динамическим.

В общем виде принцип резонанса Шумана иллюстрируется рис.1.1. Электромагнитная волна, созданная источником колебаний, начинает распространяться равномерно во все стороны, обтекая земной шар. В диаметрально противоположной точке - антиподе, пройдя по любой из дуг вдоль поверхности Земли одно и то же расстояние, она встречается сама с собой, после чего продолжает двигаться, накладываясь сама на себя. Т.о. в точке - антиподе происходит геометрический реверс волны по отношению к самой себе, что, в определенной степени, аналогично отражению волны от отражателя без потерь. Поэтому будет корректно назвать волну, движущуюся от источника к точке реверса, прямой, а движущуюся от точки реверса к источнику - обратной.

Если источник продолжает излучать электромагнитные колебания, то после прохождения волной одного полного оборота устанавливается режим, при котором в любой точке пространства между земной поверхностью и ионосферой присутствуют две когерентные волны (т.е. имеющие одну и ту же частоту и постоянную разность фаз), двигающиеся во встречных направления вдоль дуги, соединяющей источник электромагнитных колебаний с его географическим антиподом. Если при этом они делают полный оборот вокруг Земли за целое число периодов, то в пространстве Земля - ионосфера возникает стоячая волна.

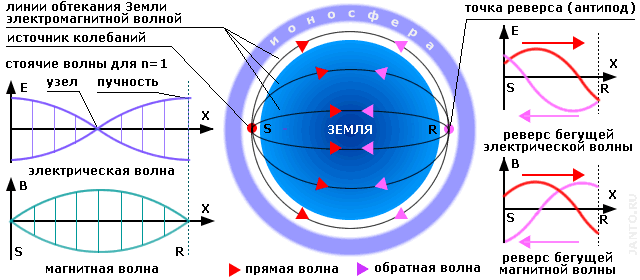
Рис.1.1. Принцип резонанса Шумана

 

Вектор электрической компоненты резонанса Шумана направлен вертикально, поэтому его ориентация не изменяется при изменении азимутального направления движения волн в рассматриваемом волноводе. В результате в точке реверса и в точке источника амплитуды прямой и обратной электрических волн совпадают как по величине, так и по знаку, вследствие чего суммируются и создают пучности. Это подтверждается математическим выражением для суммы прямой и обратной синфазных волн (без учета потерь и изменения сечения волновода - см. ниже):

 

[1] sin(ωt + X) + sin(ωt - X) = 2 sin(ωt) cos(x)

 

где:

sin(ωt + X) - амплитуда прямой волны c круговой частотой ω в момент t точке X;

sin(ωt - X) - амплитуда обратной волны c круговой частотой ω в момент t в точке X.

 

Как видно, максимальные значения амплитуд данной стоячей волны изменяются вдоль оси X по закону косинуса, т.е. на концах полуволновых интервалов располагаются пучности, что соответствует левой верхней диаграмме рис.1.1. При этом напряженность поля в каждой точке оси X меняется во времени по синусоидальному закону.

Вектор магнитной составляющей электромагнитной волны всегда ортогонален вектору электрической, поэтому в данном случае будет горизонтален. В связи с этим векторы магнитных волн, излучаемых в точке S в диаметрально противоположных направлениях, будут противофазны. Эта противофазность сохранится и до момента их встречи в точке R и будет сохраняться далее в течение всего цикла встречного движения. Поэтому в точках S и R амплитуды прямой и обратной магнитной волны будут равны, но противоположны по знаку, что приведет к образованию в данных точках узлов стоячей волны. При этом уравнение [1] примет вид:

 

[2] sin(ωt + X) - sin(ωt - X) = 2 cos(ωt) sin(x)

 

что соответствует левой нижней диаграмме рис.1.1.

 

Как видно, электрическая и магнитная волна резонанса Шумана сдвинуты относительно друг друга на четверть длины в пространстве и на четверть периода во времени. Динамика процесса формирования компонентов стоячей волны иллюстрируется рис.1.2. на примере второй гармоники резонанса.

 

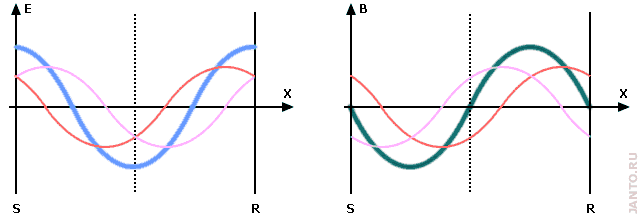
Рис.1.2. Формирование волн второй гармоники резонанса Шумана

Слева - электрическая волна, справа - магнитная. Цвета стоячих, а также прямой и обратной бегущих волн соответствуют цветам рис. 1.1. Кнопка «пуск» запускает анимацию, кнопка «стоп» возвращает диаграмму в исходное статическое состояние.

 

 

 

На рис.1.3. показаны трехмерные статические модели стоячих волн резонанса Шумана для первой - третьей гармоник (за основу взяты изображения моделей из презентации к обзорному докладу сотрудника ЕКА С.Т.Редондо «Резонанс Шумана в полости Земля - ионосфера» - см. приложение B).

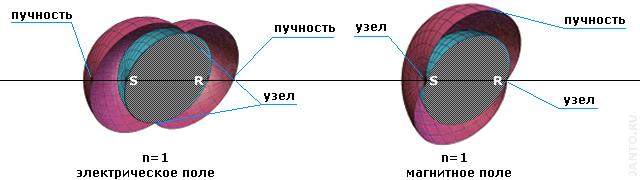
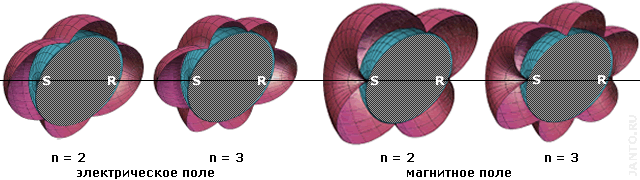
для переключения между моделями первой и второй/третьей гармоник кликните по рисунку

Рис.1.3. Трехмерные модели резонанса Шумана

 

Еще одной особенностью резонанса Шумана, обусловленной геометрией его волновода, является специфическая зависимость напряженности поля от расстояния. Если в случае источника волн, находящегося в свободном пространстве, она убывает пропорционально квадрату расстояния, то в рассматриваемом волноводе она первую половину пути от источника к точке реверса убвает, а далее - возрастает, причем, в случае идеального волновода без потерь, возрастает до первоначального значения. То же происходит и с напряженностью поля обратной волны. Причина данного явления заключается в том, что площадь поперечного сечения волновода растет по мере удаления от источника и точки реверса и достигает максимума в середине интервала между ними, где диаметр сечения волновода максимален (рис.1.4). Соответственно, учитывая, что волна занимает весь объем волновода, плотность энергии будет уменьшаться по мере приближения к середине интервала.

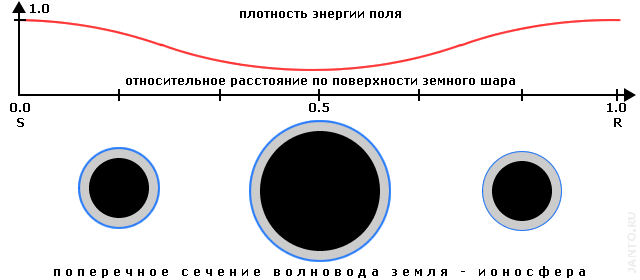
Рис.1.4. Зависимость напряженности поля резонанса Шумана от расстояния
(для идеального волновода)

 

Для учета данной вариации в приведенных выше формулах [1] и [2] необходимо ввести дополнительный коэффициент K(X) <= 1.0, принимающий максимальное значение (1.0) в точках S и R и минимальное - в середине интервала. На трехмерных диаграммах рис.1.3 влияние площади сечения волновода учтено, что видно при сравнении амплитуд.

Площадь поперечного сечения волновода равна площади усеченого конуса с образующей, равной высоте волновода Земля - ионосфера, и радиусами оснований, равными RзCos(α) и RиCos(α), где Rз и Rи - радиусы Земли и ионосферы соответственно, а α - значение значение географической широты сечения волновода относительно «экватора» - окружности, равноудаленной от точек источника S и его антипода (точки реверса) R. Как видно, площадь поперечного сечения изменяется по косинусоидальному закону, из чего можно было бы сделать предположение, что и плотность энергии также будет изменяться по косинусоидальному закону. Однако данное предположение требует проверки расчетом, что выходит за рамки настоящей главы. Результаты современного компьютерного моделирования изменения амплитуды магнитного поля в зависимости от расстояния можно посмотреть в приложении B. Следует также отметить, что в большинстве источников, описывающих основы резонанса Шумана, данный эффект может вообще не упоминаться.

 

Упрощенный расчет частот резонанса Шумана может быть сделан исходя из условия, что электромагнитная волна должна укладываться на длине окружности земного шара целое число раз, при этом потери в волноводе отсутствуют. С учетом этого имеем следующее выражение для частоты резонанса:

 

[3] f = Cn/2πRз = 7.5n,

 

где n - номер гармоники резонанса, С = 300000 км/с - скорость света, Rз = 6370 км - радиус Земли. Ряд частот для первых пяти гармоник резонанса, вычисленных по данной формуле, приведен в таблице, и, как видно из сравнения с фактическими значениями, дает погрешность, возрастающую с ростом частоты. Одна из причин этого заключается в том, что упрощенный расчет базируется на евклидовой геометрии, использование которой для сферических форм не совсем корректно. Поэтому первым шагом в совершенствовании математической модели является использование аппарата сферической геометрии, в т.ч. полиномов Лежандра для описания волн. Результатом является следующее выражение для частот:

 

[4] f = (C/2πRз)√n(n+1) = 7.5 √n(n+1) Гц.

 

Данное выражение дает ряд частот с еще большей погрешностью (см. таблицу). Причина заключается в том, что оно справедливо для волновода с идеально токопроводящими стенками. Поверхность Земли в первом приближении удовлетворяет этому условию, чего не скажешь об ионосфере, потери в которой замедляют скорость электромагнитных волн, понижая частоты резонанса. В.О.Шуман учел данный фактор, введя в формулу [4] для идеального волновода без потерь делитель Re(σ), представляющий собой действительную часть комплексного показателя рефракции ионосферы, и получил следующее выражение:

 

[5] f = [C/2πRзRe(σ)]√n(n+1) = [7.5/Re(σ)] √n(n+1) Гц.

 

Данная формула дает существенное приближение расчетных значений частот ряда к фактическим в области высших гармоник (см. таблицу), но погрешность в области низших, особенно на первой гармонике, все еще остается значительной. Это обусловлено тем, что реальные значения показателя рефракции ионосферы изменяются с изменением высоты, поэтому современный математический аппарат предусматривает использование моделей, учитывающих данное изменение, в частности, двухступенчатой (двухвысотной) линейной модели (подробнее см. в приложении А).

Расчетные и фактические частоты резонанса Шумана

модель	ряд частот с 1-й по 5-ю гармоники, Гц
идеальная евклидова	7,5   -   15,0   -   22,5   -   30,0   -   37,5
идеальная сферическая	10,6   -   18,4   -   26,0   -   33,5   -   41,1
сферическая Шумана (с потерями)	8,5   -   14,7   -   20,8   -   26,8   -   32,9
фактически	7,8   -   14,1   -   20,3   -   26,4   -   32,4

 

В последние годы появляются новые, более точные модели резонанса, расчитываемые на мощных ЭВМ, например, TLM (Transmission-Line Modelling). Кроме того, делаются попытки применить для расчета вместо классических уравнений Максвелла аппарат квантовой электродинамики. Данные направления будут рассмотрены в отдельной главе.

Указанные в таблице фактические частоты являются средними значениями центральных частот спектров гармоник, полученными по данным большого числа измерений. Текущие значения не являются стабильными и зависят от многих факторов, в первую очередь от параметров ионосферы (см. рис. 1.5).

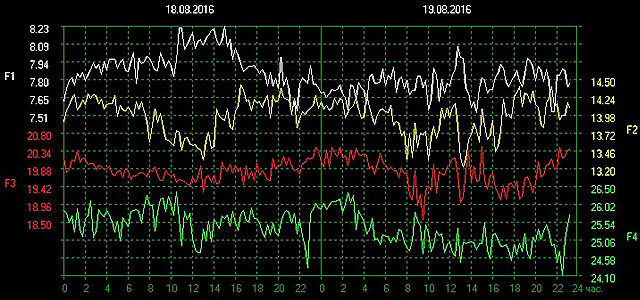
Рис.1.5. Вариации частот первых четырех гармоник резонанса Шумана
(данные Томской станции мониторинга)

 

Периодически появляющиеся в популярных публикациях сенсационные сведения о том, что частота резонанса, якобы, неожиданно пошла в рост, не имеют под собой никаких объективных оснований, что будет показано далее при анализе данных мониторинга.

 

На рис. 1.6. приведен типичный спектр регистрируемых естественных электромагнитных колебаний в полосе частот, соответствующих диапазону резонанса Шумана (представлена горизонтальная магнитная составляющая). Резонансам соответствуют пики спектра на частотах f1 - f7.

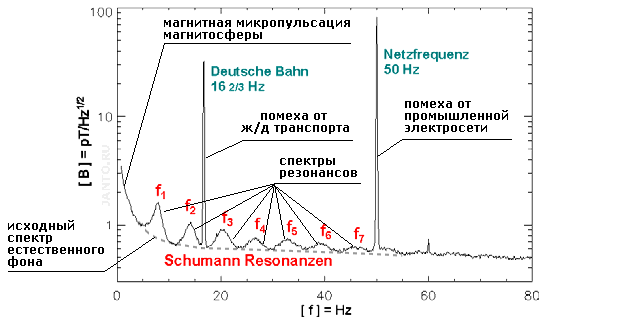
Рис.1.6. Спектр колебаний в полосе частот резонанса Шумана

(за основу взята иллюстрация из статьи К.Шлегеля и М.Фюллекруга «50 лет резонансу Шумана»)

 

Как видно, наибольшим абсолютным и относительным уровнями сигнала обладает первая гармоника, при этом с повышением частоты резонанс становится все менее выраженным, практически полностью затухая на частотах выше 60-70 Гц. Максимальное превышение сигнала резонанса на центральных частотах гармоник над фоном невелико. Это является следствием невысокой добротности резонатора Земля-ионосфера, из-за чего чего спектры гармоник размыты в достаточно широкой полосе частот. Амплитуды сигналов, также, как рассмотренные выше частоты, нестабильны во времени. Изменяется также ширина спектра (добротность) сигналов. Вид типовой спектральной характеристики гармоник и примеры графиков их амплитуд приведены на рис. 1.7.

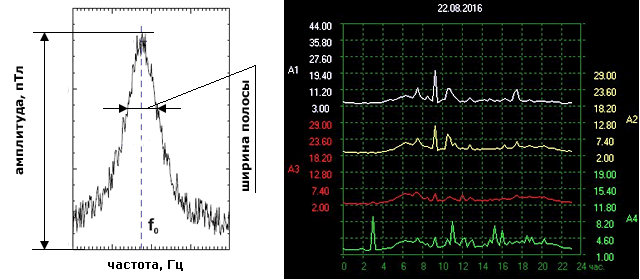
Рис.1.7. Параметры спектра и амплитуда колебаний резонанса Шумана

(за основу взята иллюстрация из статьи К.Шлегеля и М.Фюллекруга «50 лет резонансу Шумана» и данные Томской станции мониторинга)

 

Более подробные сведения о параметрах колебаний резонанса Шумана, их измерении, обработке и мониторинге см. в следующих главах.

* * * * *

 

 

Опубликовано 24.08.2016. Последнее изменение - нет.

© Janto 2016 Все права защищены